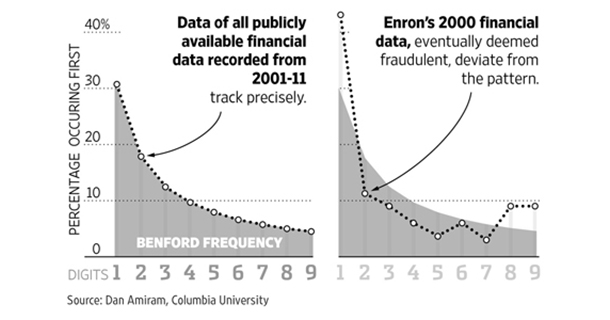
引子
假设某银行有许多储户,他们账户上的存款余额不等。如果这些储户来自于一个财富水平随机且服从均匀分布的大样本,则从他们存款余额的所有数据中随机选取一个,该数据以数$1$为首位的概率是多少?
面对这个问题,大部分人可能会不假思索地回答$1/9$,因为这些数据来自于一个随即且均匀的样本,那么从$1$到$9$,以这些数为首位的概率是相等的,为$1/9$。
但事实上,大量从真实数据集观察到的结果却与这一看似理所当然的推测大相径庭,以数$1$为首位的数据出现的频率要比其他数字大得多,这一比例甚至超过了30%,而以数$9$为首位的数据出现的频率则只有5%不到。
这表明,自然数数据集首位数字出现概率的真实分布其实并不如我们想当然的那样。在数学中,这一现象有一个专门的名称——它被人们称为本福特定律(Benford’s Law)。
本福特定律
事实上,本福特定律表明,在$b$进位制下,在一个跨越多个数量级的大容量随机样本中,以数$n, n=1,2,\cdots, n-1$为首位的数据出现的概率为:
例如在十进制中,以数(1)为首位的数据出现的概率为:
在自然数集不受人为因素干扰的情况下,以各个数字为首位的数据出现的概率分别为:
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ |
| $P(n)$ | 30.1% | 17.6% | 12.5% | 9.7% | 7.9% | 6.7% | 5.8% | 5.1% | 4.6% |
历史
尽管这一定律被称为本福特定律,但事实上本福特并非第一个发现它的人。
1881年,天文学家西蒙·纽康发现对数表包含以数$1$为首位的数字那几页较其他页破烂。
1938年,物理学家弗兰克·本福特再次发现这个现象,还通过了检查许多数据来证实这点。
2009年,西班牙数学家将本福特定律同素数分布联系到一起,计算了在一定长度的素数序列中以各个数字为首位的数据出现频率。如果素数是随机分布的,那这项研究的结果应该符合本福特定律,然而事实却并非如此。该分布与本福特定律存在着明显差异,它也可以被认为是素数的本福特定律。
条件
尽管基于大量数据集的分析结果表明本福特定律是一个适用范围很广的数字规律,但该定律的应用仍有一定的前置条件:
这些数据必须跨度足够大,样本数量足够多,数值大小相差几个数量级;
按一定规则人为生成的数据很可能不满足本福特定律,例如电话号码、身份证号码、发票编号等。为造假而人工修改过的实验数据和财务数据也可能不符合本福特定律。
轶闻
基于本福特定律的前置条件,它的一个重要作用便是用来验证实验数据或财务数据的真实性。这是由于该类数据在未经人工修改的条件下满足本福特定律。
美国华盛顿州曾侦破过一个涉案金额高达1亿美元的诈骗案,以主犯凯文·劳伦斯为首的一伙人以连锁健身俱乐部为噱头,向数千名投资者募集资金,然后将这些资金用于个人消费。为了掩饰他们的不法行为,他们又将一部分资金在离岸公司和银行账户间频繁转账,并且认为做假账,向外界传达一种公司生意兴隆的错误信息。
但在当时有一名会计师将数万个与支票和汇款有关的数据收集起来并统计这些数据中每个首位数字出现的频率,结果发现它们并不满足本福特定律。于是,他向社会揭露了凯文·劳伦斯一伙的罪行,并这一发现作为佐证材料一并公之于众,最终,经过长达三年的司法调查,终于捣毁了这一诈骗团伙,主犯劳伦斯也被判处20年监禁。
回到本文开篇的图表,这分别是以美国最大能源交易商安然公司(Enron Corporation)在2000年(右)和2001年11月(左)的财务报表中的数据作为样本,并统计它们中以各个数字为首位的数据出现频率得到的。该公司在2000年发生了极其严重的财务造假行为,并最终在2001年宣告破产。如图所示,该公司在2000年的财务数据与本福特定律相去甚远,这表明这些数据可能是人为修改的结果,这也是该公司在事实上所发生的。

