朋友悖论：一个图论中的有趣结论

引子

我们在社交中很容易发现一个现象，即平均而言你的朋友总是比你拥有更多的朋友。这听起来是一件不那么好的事情，但事实确实是如此，他们所拥有的朋友确实比你多。这就是统计学中的朋友悖论(Friendship Paradox)。

简介

这一看起来不太符合常理的悖论其实是由美国社会学家Scott L. Feld在1991年首次观察到的有趣社会现象，即平均而言，一个人的朋友比这个人本身拥有更多的朋友。在统计学中，这也可以被理解为一种抽样偏差(Sampling Bias)，即一个人更有可能和那些拥有很多朋友的人是朋友，而不太可能是那些朋友少的人。
同样的关系也适用于其他范畴下的社交网络，如同事关系和性伴侣关系等等。

数学解释

在图论当中，社交网络可以被抽象为一个无向图(Undirected Graph)，每个人相当于这个图中的一个点，而朋友关系相当于两个点之间的连线。如果一个人有$d(v)$个朋友，相当于在图中有$d(v)$条边(在图论中，这也被称为该顶点的度数)和表示这个人的点相连。

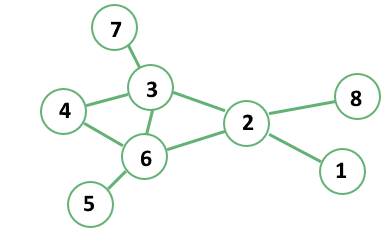
下图是无向图的一个例子：

假设在一个无向图$G = (V, E)$中，对于一个随机的点，平均而言有$\mu$条边与之相连，则我们有

$$\mu =\frac{ {\textstyle \sum_{v\in V} d(v)} }{|V|} =\frac{2|E|}{|V|}$$

而要计算平局一个人所有朋友的平均朋友数，可以通过随机选择一个人，然后计算他的朋友平均有多少朋友。这相当于在对应的无向图中，随机地选择一条边，和该边的一个端点，再计算该点的度数，即

$$\frac{1}{2}\frac{d(v)}{|E|}$$

这里之所以要乘$\frac{1} {2}$，是因为每条边都有两个顶点，我们在取遍所有边的过程中，每个顶点都会被取到两次。于是我们所要求的“每个人朋友的朋友人数的平均数”，就可以用下式来表示：

$$\textstyle \sum_{v\in V} (\frac{1}{2}\frac{d(v)}{|E|})d(v) = \frac{\textstyle \sum_{v\in V} {d(v)}^2}{2|E| }$$

由方差的定义，可得：

$$\frac{\sum_{v\in V}{d(v)}^2 }{|V|} = \mu^2 + \sigma^2$$

其中$\sigma^2$为$d(v)$的方差，由此可得：

$$\frac{\textstyle \sum_{v\in V} {d(v)}^2}{2|E| } = \frac{|V|}{2|E|}(\mu^2 + \sigma^2) = \frac{\mu^2 + \sigma^2}{\mu} = \mu + \frac{\sigma^2}{\mu}$$

由定义可得$\mu , \sigma$显然都是不小于0的常数，因此$\mu + \frac{\sigma^2}{\mu} \geq \mu$

这就在统计学上证明了这一结果，尽管这一证明过程并非完全严谨，但得出的结论也具有在现实中足够的论述力。

结语

虽然朋友悖论在统计学中被认为是一种抽样偏差，但在现实中，我们不得不承认的是，我们所感受到的满足感与落差感在大多数时候都源于身边的境况。在此时，朋友悖论告诉人们的是，如果你常常把自己同身边的朋友作比较，那你可能很难得到满意的结果，因为你总是可以很容易地在身边找到那些把自己比下去的朋友。
这一有趣的社会现象除了揭露一个听上去并不是很好的事实以外也并非毫无用处。事实上，它是一个在社会学、流行病学当中都十分有用的结论。
朋友悖论的结果表明，在社交网络中，一个随机选择的个体的朋友很可能具有高于该个体本身的中心性，这将有利于在流行病防控的过程中帮助当局筛选出那些具有较高社会活动能力的个体作为重点防控对象。
在选举结果预测中，这一结果也被用来为建模提供一种新的思路，例如在问卷中设置和被调查者朋友相关的问题来获取更多且更真实的信息。